Trigonometry Formula PDF Download (त्रिकोणमिति सूत्र) Trigonometry Chart, Sheet

Trigonometry Formula PDF यहॉ पर उपलब्ध है, तथा Trigonometry Formula PDF Download भी कर सकते है, नीचे हमने सभी Important Trigonometry Math Formula in Hindi , त्रिकोणमिति चार्ट, Trigonometry Sheet लेकर आए है, आपने बहुत सी परीक्षाओ मे देखा होगा की त्रिकोणमिति सूत्र से बहुत से प्रश्न पूछे जाते है। यहॉ पर आपको त्रिकोणमिति से सम्बन्धित पूरे सूत्र को नीचे दिए गए Button पर Click करके प्राप्त करसकते है, आज हमारी Team आपके लिए गणित से सम्बन्धित Trigonometry त्रिकोणमिति के सभी सूत्र (Formula) को PDF मे लेकर आए है, आप नीचे दिए गए Download Button पर Click करके Save/Download कर सकते है।

Trigonometry Formula

1. Changes Between Angles
2. Some Important Facts
3. If (x+y) = 90*
4. If (A+B+C) = 180*
5. Maximum & Minimum Values
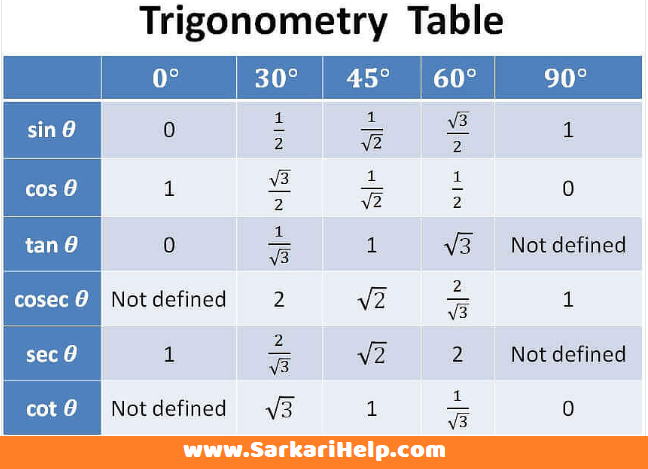
6. Trigonometric Values
7. Number System (संख्या पद्धति) Formulas

Trigonometry Formula PDF

Download Trigonometry Cheat Sheet PDF

Trigonometry All Formula

• Simple Interest SI Questions Formula

The Reciprocal Identities are given as:

• cosec θ = 1/sin θ
• sec θ = 1/cos θ
• cot θ = 1/tan θ
• sin θ = 1/cosec θ
• cos θ = 1/sec θ
• tan θ = 1/cot θ

These formulas are used to shift the angles by π/2, π, 2π, etc. They are also called cofunction identities.

• sin (π/2 – A) = cos A & cos (π/2 – A) = sin A
• sin (π/2 + A) = cos A & cos (π/2 + A) = – sin A
• sin (3π/2 – A)  = – cos A & cos (3π/2 – A)  = – sin A
• sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A
• sin (π – A) = sin A &  cos (π – A) = – cos A
• sin (π + A) = – sin A & cos (π + A) = – cos A
• sin (2π – A) = – sin A & cos (2π – A) = cos A
• sin (2π + A) = sin A & cos (2π + A) = cos A

The cofunction or periodic identities can also be represented in degrees as:

• sin(90°−x) = cos x
• cos(90°−x) = sin x
• tan(90°−x) = cot x
• cot(90°−x) = tan x
• sec(90°−x) = cos x
• cec(90°−x) = sec x

• sin(x+y) = sin(x)cos(y)+cos(x)sin(y)
• cos(x+y) = cos(x)cos(y)–sin(x)sin(y)
• tan(x+y) = (tan x + tan y)/ (1−tan x •tan y)
• sin(x–y) = sin(x)cos(y)–cos(x)sin(y)
• cos(x–y) = cos(x)cos(y) + sin(x)sin(y)
• tan(x−y) = (tan x–tan y)/ (1+tan x • tan y)

• sin(2x) = 2sin(x) • cos(x) = [2tan x/(1+tan² x)]
• cos(2x) = cos²(x)–sin²(x) = [(1-tan² x)/(1+tan² x)]
• cos(2x) = 2cos²(x)−1 = 1–2sin²(x)
• tan(2x) = [2tan(x)]/ [1−tan²(x)]
• sec (2x) = sec² x/(2-sec² x)
• csc (2x) = (sec x. csc x)/2

• Sin 3x = 3sin x – 4sin³x
• Cos 3x = 4cos³x-3cos x
• Tan 3x = [3tanx-tan³x]/[1-3tan²x]